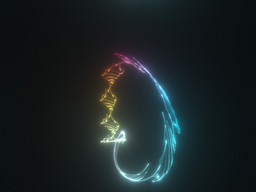See also: realtime viewer for those attractors.
More images like this
The Story:
I started my Automated Test Render #13 saturday evening and when i woke up this sunday i got about two thousands great, very varied images, with most images being totally unique. It's almost as if my software got mind of it's own and started doing art. (Well, the tests 1,2,3,4,5,6,7,8,9,10,11,and 12 also made a lot of good images, and i did see few first images before going to bed, and that's not first time it happens, but you got idea, i was amazed anyway and i hope you are too)
Check
directory listing for more and newer images, look especially for folders with "good" and "explore" in name.
Chaotic Atrractor / Fractal Equations:
That is some interesting fractal which has no name yet. It is a chaotic map, which just like my Lorenz IFS follows general formula of
X
i+1=X
i + k * f(X
i) / |f(X
i)|
where X
i is i-th point in attractor, and f is some function (which takes vector and returns vector). The formula is iterated to obtain many points X
i which are rendered as points of light of varying color using the abovementioned software.
In tests 4..13 i was trying second degree polynomials as f and doing it with 3 dimensional vectors.
It is somewhat inspired by Paul Bourke's
Random Attractors
Selection:
Fractal formulas in general do not always produce good looking images. In fact if parameters (polynomial coefficients in this case) are totally random this one only has about one in thousand chance to look remotely interesting.
I developed some automatic searcher that hops through different parameters looking for the parameters which give good images. The heruistics is somewhat long to describe and it's still in very experimental stage. I am using Lyapunov's Exponent estimate to check if it is chaotic, then some other measures to check if it is likely to be interestingly chaotic i.e. that it is not flat and is not one dimensional loop. I'm planning to add "not seen that before" heruistics, as some few shapes seems to come up relatively often.
Views:
The greatest shapes is worth nothing if camera is looking wrong way, so there's some nice camera placement algorithms aswell.
Colors:
Black and white graphics is not very visually appealing, so for this one i do some rgb coloring by coordinates.
Future:
I'm gonna make movie with it :-) (update 1: working on it, got the toolset half-ready. update 2: had absolutely no time until now and still have no time. See my "volumetrics" page for example of what i'm mostly working on) and possibly screensaver tho that might depend to some technology licensing issues. I have more good new ideas what to try than i can implement.
To be continued...